Pengertian
Fungsi eksponensial adalah fungsi matematika yang digunakan dalam banyak
situasi dunia nyata. Hal ini terutama digunakan untuk menemukan peluruhan
eksponensial atau pertumbuhan eksponensial atau untuk menghitung investasi,
memodelkan populasi, dan sebagainya. Pada artikel ini, Anda akan
mempelajari rumus fungsi eksponensial , aturan, sifat, grafik,
turunan, deret eksponensial, dan contohnya.
Apa itu Fungsi Eksponensial?
Rumus Fungsi Eksponensial
Fungsi eksponensial didefinisikan dengan rumus f(x) = a x ,
dengan variabel input x muncul sebagai eksponen. Kurva eksponensial
bergantung pada fungsi eksponensial dan bergantung pada nilai x.
Fungsi eksponensial adalah fungsi
matematika penting yang berbentuk
f(x) =a x
Dimana a > 0 dan a tidak sama
dengan 1.
x adalah bilangan real apa pun.
Jika variabelnya negatif, fungsinya
tidak terdefinisi untuk -1 < x < 1.
Di Sini,
"x" adalah variabel
“a” adalah konstanta yang merupakan
basis dari fungsi tersebut.
Kurva eksponensial bertambah atau
berkurang bergantung pada fungsi eksponensial. Kuantitas apa pun yang
bertambah atau berkurang dengan persentase tetap pada interval teratur harus
mengalami pertumbuhan eksponensial atau peluruhan eksponensial.
Pertumbuhan Eksponensial
Dalam Pertumbuhan Eksponensial, kuantitasnya meningkat sangat lambat
pada awalnya, dan kemudian dengan cepat. Tingkat perubahan meningkat
seiring waktu. Laju pertumbuhan menjadi lebih cepat seiring berjalannya
waktu. Pertumbuhan pesat dimaksudkan sebagai “peningkatan
eksponensial”. Rumus untuk mendefinisikan pertumbuhan eksponensial adalah:
kamu = a ( 1+ r ) x
Dimana r adalah persentase
pertumbuhan.
Peluruhan Eksponensial
Dalam Peluruhan Eksponensial, kuantitasnya berkurang dengan sangat cepat
pada awalnya, dan kemudian secara perlahan. Tingkat perubahan menurun
seiring waktu. Laju perubahan menjadi lebih lambat seiring berjalannya
waktu. Pertumbuhan pesat berarti “penurunan eksponensial”. Rumus
untuk mendefinisikan pertumbuhan eksponensial adalah:
kamu = a ( 1- r ) x
Dimana r adalah persentase
peluruhan.
Gambar berikut merupakan grafik
eksponen x. Dapat dilihat bahwa dengan meningkatnya eksponen, kurva
menjadi semakin curam dan laju pertumbuhan pun meningkat. Jadi, untuk x
> 1, nilai y = f n (x) bertambah seiring bertambahnya
nilai (n).
Dari penjelasan di atas terlihat bahwa sifat fungsi polinomial
bergantung pada derajatnya. Semakin tinggi derajat suatu fungsi
eksponensial , semakin tinggi pula pertumbuhannya. Fungsi yang tumbuh
lebih cepat daripada fungsi polinomial adalah y = f(x) = a x ,
dengan a>1. Jadi, untuk sembarang bilangan bulat positif n, fungsi f
(x) dikatakan tumbuh lebih cepat dibandingkan fungsi f n (x).
Jadi, fungsi eksponensial yang mempunyai basis lebih besar dari 1, yaitu
a > 1 didefinisikan sebagai y = f(x) = a x . Daerah
fungsi eksponensial adalah himpunan seluruh bilangan real R dan jangkauannya
dikatakan himpunan semua bilangan real positif.
Perlu diperhatikan bahwa fungsi
eksponensial meningkat dan titik (0, 1) selalu terletak pada grafik fungsi
eksponensial. Selain itu, mendekati nol jika nilai x sebagian besar
negatif.
Fungsi eksponensial yang mempunyai
basis 10 disebut fungsi eksponensial persekutuan. Perhatikan rangkaian
berikut ini:
Nilai deret ini terletak antara 2
& 3. Diwakili oleh e. Dengan menggunakan e sebagai basis dari fungsi
tersebut, kita mendapatkan y = e x , yang merupakan fungsi
yang sangat penting dalam matematika yang dikenal sebagai fungsi eksponensial
natural.
Untuk a > 1, logaritma b ke basis
a adalah x jika a x = b. Jadi, log a b
= x jika a x = b. Fungsi ini dikenal sebagai fungsi
logaritma.
Untuk basis a = 10, fungsi ini
disebut logaritma persekutuan dan untuk basis a = e, dikenal sebagai logaritma
natural yang dilambangkan dengan ln x. Berikut beberapa pengamatan penting
mengenai fungsi logaritma yang mempunyai basis a>1.
- Domain fungsi log hanya terdiri
dari bilangan real positif , karena kita tidak dapat menafsirkan arti
fungsi log untuk nilai negatif.
- Untuk fungsi log, walaupun
domainnya hanya himpunan bilangan real positif, rangenya adalah himpunan
semua nilai real, yaitu R
- Saat kita memplot grafik fungsi
log dan berpindah dari kiri ke kanan, fungsi tersebut menunjukkan perilaku
yang meningkat.
- Grafik fungsi log tidak pernah
memotong sumbu x atau sumbu y, meskipun cenderung ke arahnya.
- Log a p =
α, log b p = β dan log b a = µ,
maka a α = p, b β = p dan
b µ = a
- Log b pq =
Log b p + Log b q
- Log b p y =
ylog b p
- Log b (p/q)
= log b p – log b q
Sekarang mari kita fokus pada
turunan fungsi eksponensial.
Turunan e x terhadap
x adalah e x , yaitu d( ex )/dx =
e x
Diketahui bahwa fungsi eksponensial
f(x) =e x mempunyai sifat khusus. Artinya
turunan suatu fungsi adalah fungsi itu sendiri.
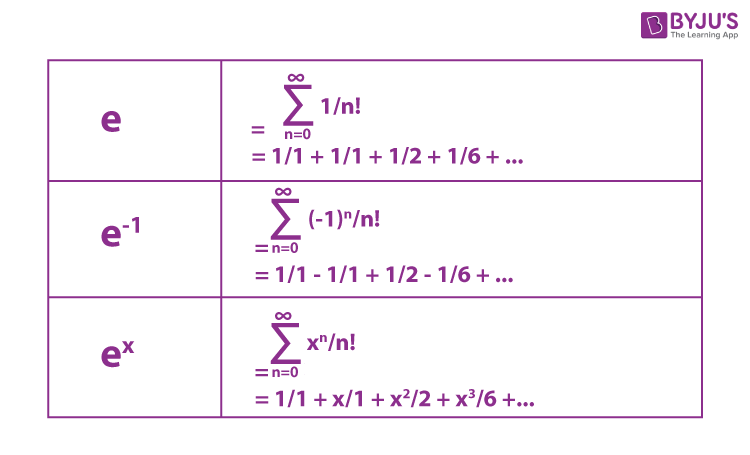
Seri Eksponensial
Deret eksponensial diberikan di
bawah ini.
Properti Fungsi Eksponensial
Grafik eksponensial suatu fungsi
mewakili sifat fungsi eksponensial.
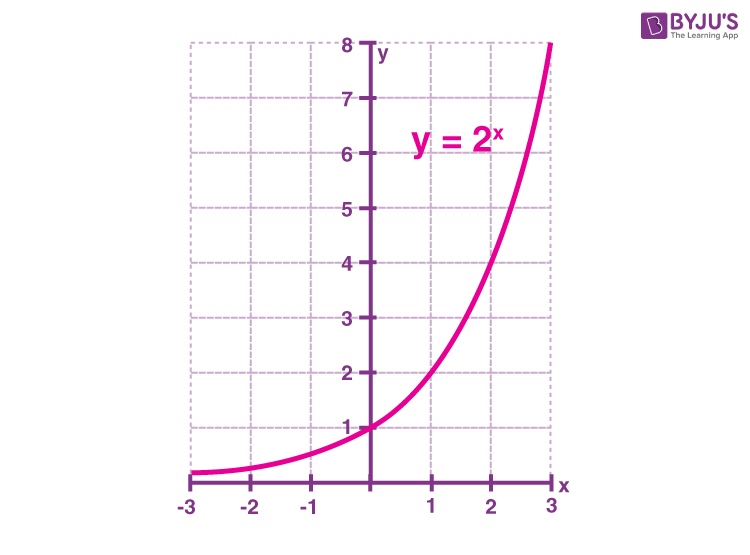
Mari kita perhatikan fungsi
eksponensial, y = 2 x
Grafik fungsi y = 2 x ditunjukkan
di bawah ini.
Grafik Fungsi Eksponensial untuk y =
2 x
Sifat-sifat grafik fungsi
eksponensial jika basisnya lebih besar dari 1 diberikan di bawah ini.
- Grafik melewati titik (0,1).
- Domainnya semua bilangan real
- Kisarannya adalah y>0
- Grafiknya semakin meningkat
- Grafiknya asimtotik terhadap
sumbu x karena x mendekati tak terhingga negatif
- Grafiknya bertambah tanpa batas
ketika x mendekati tak terhingga positif
- Grafiknya kontinu
- Grafiknya mulus
Grafik Fungsi Eksponensial y=2 -x
Grafik fungsi y=2 -x ditunjukkan
di atas. Sifat-sifat fungsi eksponensial dan grafiknya jika basisnya
antara 0 dan 1 diberikan.
- Garis melewati titik (0,1)
- Domain mencakup semua bilangan
real
- Kisarannya adalah y>0
- Ini membentuk grafik menurun
- Garis pada grafik di atas tidak
menunjukkan gejala terhadap sumbu x karena x mendekati positif tak
terhingga
- Garis bertambah tanpa batas
ketika x mendekati tak terhingga negatif
- Ini adalah grafik kontinu
- Ini membentuk grafik yang halus
Beberapa aturan eksponensial penting
diberikan di bawah ini:
Jika a>0 dan b>0, maka persamaan berikut ini berlaku untuk semua bilangan real x dan y:
·
ax ay = ax + y
·
ax /ay = ax - y
·
(a x ) y =
a xy
·
axbx = ( ab ) x
·
(a/b) x = ax / bx
·
sebuah 0 =1
·
a -x =
1/ ax
Contoh fungsi eksponensial adalah:
- f(x) = 2x
- f(x) = 1/ 2 x =
2 -x
- f(x) = 2 x+3






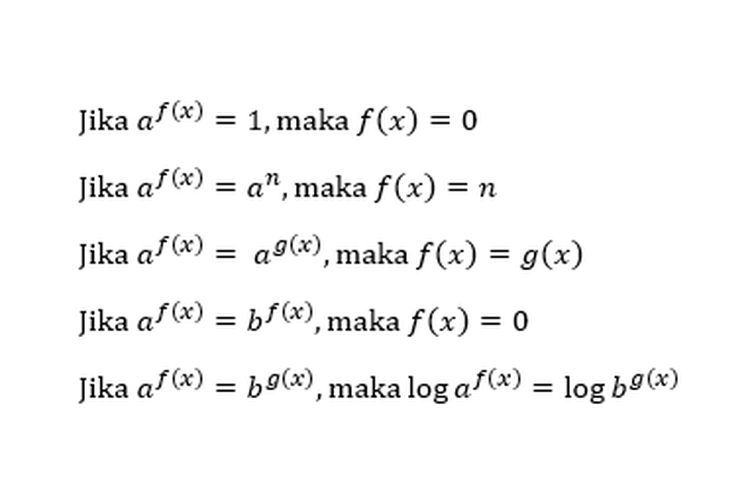






Tidak ada komentar:
Posting Komentar